期望最大化算法

对于概率模型, 我们经常会根据其观测值组成的样本数据, 通过极大似然估计, 找到其对数似然函数极大值对应的参数, 这个参数就是模型参数的极大似然估计值, 我们将其认为是通过样本训练得到的参数.

但是对于一些问题, 我们不能直接采用极大似然估计来最大化对数似然函数, 找到对应的参数值, 这是因为模型中含有隐变量(Latent Variable), 即观测不到的隐含数据变量, 此时我们未知的有隐变量和模型参数, 从而无法直接使用极大似然估计得到最终的模型.

期望最大化(Exception Maximization)算法通过启发式的迭代方法, 来解决此问题.

首先通过一个经典例子引入问题.

三硬币问题

实验描述: 有三枚硬币, 记为$A$, $B$, $C$, 对应的正面朝上的概率分别是$\pi$, $p$, $q$. 实验过程如下, 先掷硬币$A$, 如果正面朝上则再掷硬币$B$, 背面朝上则掷硬币$C$, 最后得到实验$n$的观测序列$X=\{x_1,x_2,\cdots,x_n\}$, $x_i$为第$i$次观测的结果, 1为正面, 0为背面.

实验分析: 这种情况就有一个隐变量在其中, 即硬币$A$的结果, 我们将硬币$A$的结果记为$Z=\{z_1,z_2,\cdots,z_n\}$. 此问题的概率模型有三个参数, 即三个硬币正面朝上的概率, 我们将参数记为$\theta=\{\pi,p,q\}$.

参数求解: 想通过概率模型的对数似然函数来对参数进行极大似然估计, 首先构造对数似然函数.

• 第$i$次观察到投掷硬币的结果为$x_i$的概率为:

  $P(x_i;\theta)=\sum\limits_{\mathbb{Z}}P(x_i|z_i;\theta)P(z_i;\pi)=\pi p^{x_i}(1-p)^{1-x_i}+(1-\pi)q^{x_i}(1-q)^{1-x_i}$

  其中$\mathbb{Z}$是集合$Z$的取值空间, 即$\{0, 1\}$.

• 构建似然函数:

  $L(\theta)=\prod\limits_{i=1}^n P(x_i;\theta)$

• 变换成对数似然函数:

  $\mathcal{L}(\theta)=\sum\limits_{i=1}^n \log{P(x_i;\theta)}$

• 求导, 令导数为零, 构建似然方程:

  $\frac{\partial \sum\limits_{i=1}^n \log[\pi p^{x_i}(1-p)^{1-x_i}+(1-\pi)q^{x_i}(1-q)^{1-x_i}]}{\partial \theta}=0$

可以看到, 对于包含隐函数的情况, 在对数似然函数内部的$\log$中, 包含着参数之间加和,导致无法求出解析解. 因此需要使用EM算法分布迭代求解.

EM算法

EM算法是一种迭代算法, 每次迭代由两步组成:

• E步: 求期望. 这一步的作用就是合理地猜想隐变量的情况

• M步: 极大似然求解参数. 即根据观测数据和猜测的隐变量来极大化对数似然函数, 求解模型参数.

由于每一步我们的隐变量都是猜测的, 所以得到的模型参数一般不是真正的结果. 但随着迭代的进行, 算法逐渐收敛, 最终就能得到我们需要的模型的参数.

EM算法的推导过程如下:

$m$个观测样本$\{x_1,x_2,\cdots,x_m\}$, 模型的参数集为$\theta$. 极大化对数似然函数, 求模型参数:

$\arg\max\limits_{\theta}\sum\limits_{i=1}^m \log P(x_i|\theta)$

我们是无法直接求解$\theta$值的. 但由于每次观测$x_i$都对应这一次隐变量$z_i$, 假设$z_i$的取值空间为$Z$(对于上面的例子, 取值空间就是硬币$A$的正反两种情况, 且对于每个观测, 其取值范围是固定的), 用$z _{j}$表示$j$种取值情况. 因此, $P(x_i|\theta)$就可以表示为考虑所有隐变量情况的条件概率的加权和, 加权值为隐变量的概率, 即:

$P(x_i|\theta)=\sum\limits_{j=1}^{Z} P(x_i,z_{ij}|\theta)$

那么对数似然函数可以转换为:

$\mathcal{L}(\theta)=\sum\limits_{i=1}^m \log P(x_i|\theta)=\sum\limits_{i=1}^m \log \sum\limits_{j=1}^{Z} P(x_i,z_{ij}|\theta)$

现在我们的目标是求出极大化上式右侧对应的参数, 但是不能直接对之求导计算得到. 但换一个思路, 如果我们能找到一个函数, 这个函数是对数似然函数$\mathcal{L}(\theta)$的下界, 而且这个下界函数是能够通过极大似然的方法求解的, 那么我们就可以通过求下界函数的极大值来逼近对数似然函数的极大值.

同时, 我们将模型的参数集$\theta$分成两部分, 部分参数是只与隐变量相关的, 记为$\theta_z$; 其余部分隐变量确定后, 影响观测分布结果的参数, 记为$\theta_x$, 即$\theta=\{\theta_x, \theta_z\}$.

因此对于隐变量, 我们可以假设它服从分布$Q(z|\theta_z)$.

为了达到上述目的, 使用詹森不等式, 由于函数$f(x)=\log x$是凹函数, 因此有:

$\begin{aligned} \mathcal{L}(\theta) &= \sum\limits_{i=1}^m \log \sum\limits_{j=1}^{Z} P(x_i,z_{j}|\theta) \\ &= \sum\limits_{i=1}^m \log \sum\limits_{j=1}^{Z}Q(z_j|\theta_z)\frac{P(x_i,z_{j}|\theta)}{Q(z_j|\theta_z)} \\ &\ge \sum\limits_{i=1}^m\sum\limits_{j=1}^{Z}Q(z_j|\theta_z)\log\frac{P(x_i,z_{j}|\theta)}{Q(z_j|\theta_z)} \end{aligned}$

因为$Q$是分布概率, 所以$\sum\limits_{j=1}^{Z}Q(z_j|\theta_z)$是一定为1的, 使用詹森不等式在凹函数上的规则, 通过上面的推导, 我们就得到了所需要的下界函数.

对于这个下界函数, 如果能使对数似然函数$\mathcal{L}(\theta)$与其下界函数相等, 那么可以使下界函数(关于$\theta$的函数)增大的$\theta$也可以使$\mathcal{L}(\theta)$增大. 因此使下界函数达到极大值的$\theta$也是使得$\mathcal{L}(\theta)$达到极大值的$\theta$.

为了使两者相等的前提条件成立, 需要詹森不等式取等号, 而只有在$\frac{P(x_i,z_{j}|\theta)}{Q(z_j|\theta_z)}$为常数的时候才能得到, 因此有:

$\frac{P(x_i,z_{j}|\theta)}{Q(z_j|\theta_z)}=c, \quad \text{c is a constant}$

那么求下界函数的极值的阻碍就剩下了未知的$Q(z|\theta_z)$, 即隐变量的分布情况. 通过上面的常数等式, 以及$\sum\limits_{z}Q(z|\theta_z)=1$的条件, 如下推导:

$P(x_i,z_{j}|\theta)=cQ(z_j|\theta_z)$

两边对$z_j$的所有情况求和得到:

$\sum\limits_{j=1}^Z P(x_i,z_j|\theta)=c\sum\limits_{j=1}^Z Q(z_j|\theta_z)=c$

带入到$\frac{P(x_i,z_{j}|\theta)}{Q(z_j|\theta_z)}=c$, 得到:

$\sum\limits_{j=1}^Z P(x_i,z_j|\theta)=\frac{P(x_i,z_{j}|\theta)}{Q(z_j|\theta_z)}=c$

因此有:

$Q(z_j|\theta_z)=\frac{P(x_i,z_{j}|\theta)}{\sum\limits_{j=1}^Z P(x_i,z_j|\theta)}=\frac{P(x_i,z_{j}|\theta)}{P(x_i|\theta)}=P(z_i|x_i,\theta)$

因此隐函数的分布$Q(z|\theta_z)$就是在参数$\theta$下, 给定观测$x$之后的后验分布.

至此, EM算法中的E步完成, 即寻找到了隐变量的分布情况.

在得到了隐函数的分布$Q$之后, 就能更新下界函数, 由于此时对数似然函数$\mathcal{L}(\theta)$直接就是下界, 因此我们的目标变成:

$\arg\max\limits_{\theta}\mathcal{L}(\theta)=\arg\max\limits_{\theta}\sum\limits_{i=1}^m\sum\limits_{j=1}^{Z}Q(z_j|\theta_z)\log\frac{P(x_i,z_{j}|\theta)}{Q(z_j|\theta_z)}$

这也就是EM算法中的M步, 在隐变量的分布确定之后, 再通过极大似然法估计出此步的参数值$\theta$.

找到$\theta$值之后, 又可以根据参数值和公式$Q(z_j|\theta_z)=P(z_i|x_i,\theta)$求出新的隐变量的分布, 然后继续更新参数值$\theta$. 如果迭代直到收敛.

总结EM算法可以写成如下步骤:

• 初始化模型的参数值$\theta$

• 反复迭代直到收敛:

  • E步: $Q(z_j|\theta_z)=P(z_i|x_i,\theta)$

  • M步: $\theta := \arg\max\limits_{\theta}\sum\limits_{i=1}^m\sum\limits_{j=1}^{Z}Q(z_j|\theta_z)\log\frac{P(x_i,z_{j}|\theta)}{Q(z_j|\theta_z)}$

EM算法的收敛证明

参考EM算法原理总结的第四节EM算法的收敛性思考.

理解EM算法

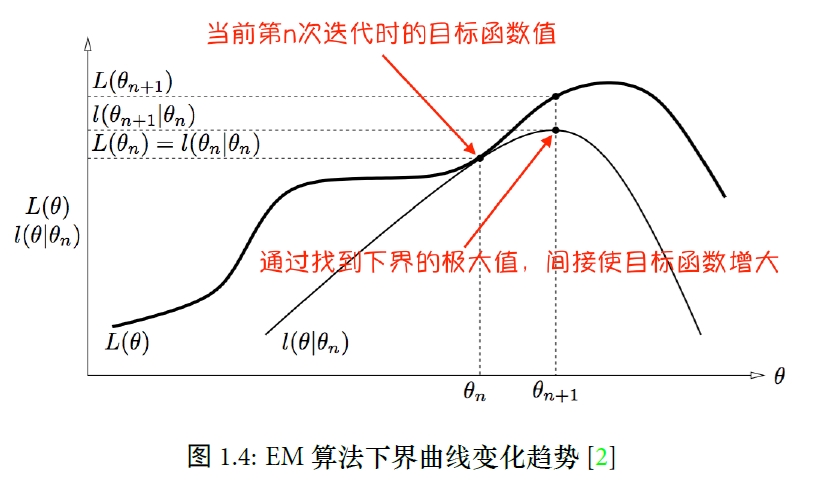
如上图所示:

• 在第$n$次迭代的E步, 在确定隐变量分布的过程中, 完成了对数似然函数和下界函数在参数$\theta=\theta_n$时的重合, 即此时的下界函数的值就是对数似然函数的值.

• 因此如果能使下界函数提高, 一定能使对数似然函数提高. 因此在M步中, 通过极大似然, 找到了$n+1$步的参数$\theta=\theta_{n+1}$, 此时的对应的对数似然函数为$L(\theta_{n+1})$, 可以从图中看到, 经过一步结点, 对数似然函数的值有了提升.

• 因此下一步又来到了E步, 在新的参数$\theta=\theta_{n+1}$点下, 得到隐变量的分布, 那么下界函数在$\theta=\theta_{n+1}$这一点又会与对数似然函数重叠在一起(在图中没有标出). 重复上面两步, 最后收敛时对应的参数, 就是我们需要的参数.